(Originally posted on Saturday, 22 June 2019)
I was inspired to create this post by a great French animated series that in English is called “Once Upon a Time – The Discoverers”:
https://en.wikipedia.org/wiki/Once_Upon_a_Time..._The_Discoverers
The Polish DVD box set (6 DVDs containing 26 episodes) looks like this:
Currently we (me, my wife and our children) watch this series and my 10-year-old daughter loves it because she can learn about many interesting things that she didn't know before. However, because it's a series for children some things are only described as fun facts, but not really explained.
For example my daughter was VERY surprised that a big (heavy) stone would fall down in the same time as a small (light) stone dropped from the same height at the same moment. This fact was shown in the episode about Galileo. I like physics very much, so I stopped the episode there and added another trivia – I told my daughter that in vacuum (without air resistance) a feather would fall down also in the same time. She couldn't believe it. The problem is that this fact (about the falling stones) was not really explained. The very next episode about Newton described among other things Newton's law of universal gravitation, which actually makes the case of the falling stones even less intuitive.
Please remember that all the pictures below are NOT to scale! Either the effects are overstated (to be visible) or the distances between orbiting moons/planets are shortened (to be visible on a small picture). I found most of the pictures on the net, but I modified some of them and I made some other totally by myself.
1. Gravity and acceleration.
Newton's law of universal gravitation is this:
F is the force between the masses,
G is the gravitational constant,
m1 is the first mass (for example the Earth),
m2 is the second mass (for example a stone),
r is the distance between the centers of the masses.
The formula is clear – the force of gravity is actually bigger when the mass of the stone is bigger, so why all the stones should fall with the same acceleration? The answer is: because a bigger (heavier) stone is harder to move than a smaller (lighter) stone. The formula for acceleration is this:
So, by combining the formula for acceleration for the mass of a stone (m2) with the formula for the force of gravity between the Earth (m1) and the stone (m2) we get this formula for the acceleration of the stone:
The acceleration of the stone (or of any other object) caused by the Earth depends only on the mass of the Earth (which doesn't change) and the distance between the Earth and the accelerated object.
BUT there is an additional catch – the force of gravity works both ways. It means that a stone accelerates towards the Earth and the Earth accelerates towards the stone, so the formula for the total acceleration is this:
The mass of a stone that weighs 1kg is 5972200000000000000000000 times smaller than the mass of the Earth, so the acceleration of the Earth toward the stone is undetectable. This is why the gravitational acceleration of “normal” objects depends ONLY on the mass of the Earth and this is why stones of different weights fall to Earth with the same acceleration.
However with more massive objects, like the Moon, the above formula becomes very important. Well, the formula would work directly only if the Moon were falling directly to the Earth. But in reality the Moon “orbits” the Earth, so what the above formula really means? It means that both the Moon and the Earth orbit their barycenter (the center of mass of two or more bodies). The barycenter of the Earth and the Moon is actually located within the Earth, but NOT at the center of the Earth. Here's a GIF showing how the Moon and the Earth orbit their barycenter:
2. Centrifugal force.
The next natural question is “why the Moon is not falling to the Earth”? This question was actually “explained” in the episode about Newton (that comes right after the episode about Galileo), but the “explanation” didn't really explain anything. The “explanation” was “The Moon is not falling to the Earth because of the centrifugal force that exists because the Moon orbits the Earth.” Oh, boy. In other words the “explanation” was this: “The Moon is not falling to the Earth because it orbits the Earth”. Obviously there is another question: “Why does the Moon orbit the Earth?”
Interestingly, the correct answer is kind of ironic: The Moon “orbits” the Earth (“the Moon is not falling to the Earth”) because the Moon keeps “falling” behind the horizon of the Earth. Imagine yourself throwing a stone in vacuum (without air resistance). A weak throw would give the stone low velocity (speed plus its vector) and the stone would fall to the ground close to you. A stronger throw would give the stone higher velocity and the stone would fall to the ground much farther. Throwing a stone with enough force would give the stone enough velocity to keep falling behind the horizon (to orbit the Earth). Even stronger throw would actually be enough to escape from the gravitational influence of the Earth.
This explains that the centrifugal force depends on the velocity. On the picture below you have a “down-to-Earth” example – a person holds an object on a string:
If the speed of the object were too low there would be not enough centrifugal force and the object would not rotate around the person in the air but it would be dragged on the ground (in space the Moon would fall to the Earth). If the speed of the object were too high the string would break and the object would fly away from the person (in space the Moon would escape from the gravitational influence of the Earth). Only if the speed were not too low and not too high the object would rotate around the person in the air without breaking the string (in space the Moon would “orbit” the Earth because the force of gravity and the centrifugal force would be equal). Please remember that the Moon and the Earth actually orbit their barycenter, so there would be two centrifugal forces – one for the Moon and the other for the Earth. I'll get back to this issue later (in part 3 about tides).
Please notice that not only the velocity has to be right (not too low and not too high), but also its vector has to be right. However, the vector of the velocity doesn't have to be perpendicular to the vector of the gravity force all the time (like in the example with the object on a string). In fact most of the orbits of the objects in space are elliptical. Here's an example of extremely elliptical orbits around a barycenter:
The orbits of The Moon and the Earth around their barycenter are elliptical too, but to a much lesser extent. However, their elliptical orbits are significant enough to make the difference between a total solar eclipse and an annular solar eclipse.
Summing up: The centrifugal force is sometimes called fictitious/pseudo force because it acts on masses whose motion is described using a non-inertial frame of reference – in this case a rotating frame of reference:
An example of a non-rotating non-inertial frame of reference would be a bus that is breaking (slowing down). The force that “pushes” the passengers towards the front of the bus is a counterpart of the centrifugal force in a rotating frame of reference. As I described above (the part about thrown stones) the same effect can be explained by sheer acceleration and velocity while “looking from the outside.” Here's a GIF:
To understand how it works you have to realise that acceleration CHANGES velocity, but not necessarily increases speed. Velocity is speed plus its vector, not speed alone. In case of orbiting objects acceleration changes mostly the VECTOR of the speed. Well, in case of a perfectly circular orbit the acceleration changes ONLY the vector of the speed, but in case of an elliptical orbit the acceleration changes mostly the vector of the speed and to lesser extent the speed itself (the speed increases when close to the barycenter, but decreases when away from the barycenter).
Interestingly, the force of gravity itself can also be seen as a fictitious/pseudo force, but it's quite complicated because it concerns curved spacetime. I will describe it in the point 4, but first let's take a look at something that is clearly visible in our world – tides.
3. Tides.
Tides are the result of the gravity of the Moon and to lesser extent of the gravity of the Sun. We could also say that tides are the result of Earth's acceleration around Moon-Earth barycenter and to lesser extent of Earth's acceleration around Sun-Earth barycenter.
First, let's understand why the gravity of the Earth doesn't cause tides on its own. The gravity of the Earth is more or less the same, so the acceleration all over the Earth is more or less the same. The only difference is the fact that the centrifugal force of the rotating Earth is slightly counteracting the gravity of the Earth, but the centrifugal force is strongest at the equator:
So the gravity at the equator is slightly lower than it is at the geographical poles. It can be compared to a child's toy ball that you squeeze with your hands, putting one hand at the top and the other at the bottom. This fact explains why the Earth is a little flattened:
The point is that the Earth is constantly rotating, so it's constantly flattened. Interestingly the Earth is constantly flattened both as a solid rock and as a mass of water. It means that some oceans are deeper than the other, but we don't see it because all the depths don't change over time because of Earth's rotation:
A very important question is this: “If here is a centrifugal force, then why all the oceans don't fly away into space?” Because the centrifugal force is very weak when compared to the force of gravity, so the centrifugal force can only slightly deform the Earth (both as a solid rock and as a mass of water). The gravity holds everything together, but this “everything” exists in a slightly flattened form caused by the centrifugal force. It can be compared to a child's toy ball that you squeeze with your hands, but the toy ball doesn't break just because you squeeze it.
So, there would be no tides without the Moon and without the Sun. But how the Moon or the Sun cause tides on the Earth? There are two explanations based either on accelerations and velocity or on the gravity and the centrifugal force. Let's start with accelerations because it's more fun and less intuitive.
3a. Tides explain by accelerations and velocity.
Let's imagine the Earth and the Moon are getting closer to each other (there is no orbit at all, but the Earth is still rotating around its axis of rotation, so the tides caused by the Moon are real). Please remember that the pictures below show only the real tides (they now ignore the different depths of ocean's caused by the centrifugal force that were shown on the previous picture). Please, notice also that the Earth's axis of rotation is tilted to the Moon's orbit plane. On the pictures below I omitted the acceleration of the Moon caused by the Earth, because there are no oceans on the Moon, so there are no tides there:
The ocean that is (at a particular moment) on the right side of the Earth is closer to the Moon than the center of the Earth and the center of the Earth is (at a particular moment) closer to the Moon than the ocean on the left side of the Earth. As I described earlier the acceleration of any object caused by the Moon depends only on the mass of the Moon (which doesn't change) and the distance between the Moon and the accelerated object. So the accelerations are different for the “right” ocean, the center of the Earth and the “left” ocean.
Because of the differences in accelerations the “right” ocean is getting closer to the Moon more quickly than the other parts of the Earth, so its acceleration is getting more and more bigger than the other accelerations, which stretches the oceans more and more with every second:
The example above shows that tides are all about accelerations, but in reality the Earth and the Moon are NOT getting closer to each other, but orbit their barycenter. So, how tides actually work? I have to repeat again: acceleration CHANGES velocity, but not necessarily increases speed. Velocity is speed plus its vector, not speed alone. In case of orbiting objects acceleration changes mostly the VECTOR of the speed.
At a particular moment the speed of the Earth around the Earth-Moon barycenter is the same for all its parts. Why? Because the Earth doesn't ROTATE around the barycenter (the Earth rotates only around its own axis of rotation), but instead the Earth moves through space (around the barycenter) as one solid object. This object (the solid rock plus the mass of water) is held together by the acceleration caused by the Earth (by its mass). The acceleration caused by the Moon is very weak when compared to the acceleration caused by the Earth, so the acceleration caused by the Moon can only slightly deform the acceleration caused by the Earth. Obviously this effect is strongest when the Earth, the Moon and the ocean are in the same line, so in the parts of the Earth that are farther away from the Earth-Moon line the effect is weaker. It slightly deforms the Earth in the Earth-Moon line (mostly the mass of water on the surface of the solid rock). It can be compared to a cherry (with the stone still inside) that you squeeze with your fingers. The cherry can be slightly squeezed, but it doesn't break just because you squeeze it AND you can't squeeze the stone inside. On the picture below I omitted the acceleration of the Moon caused by the Earth, because there are no oceans on the Moon, so there are no tides:
So, the same velocity is changed by different accelerations working at different distances away from the Moon. The formula for the centripetal acceleration is this:
So, with the same velocity and different accelerations the radii HAVE to be different. The “right” ocean has a higher acceleration, so its radius is smaller. The “left” ocean has the smallest acceleration, so its radius is the biggest. As I said earlier – everything is held together by the acceleration caused by the Earth, only slightly deformed by the acceleration caused by the Moon.
As the Earth rotates around its own axis of rotation, different oceans become “right” or “left” oceans, so over time different oceans are stretched towards or away from the Moon. Standing at a particular place at the edge of a particular ocean we see it as tides, coming and going.
3b. Tides explained by the gravity and the centrifugal force.
The explanation for tides based the gravity and the centrifugal force is more intuitive, except for one thing – the direction of the centrifugal force is the same for all parts of the Earth (exactly like velocity), even though the Earth-Moon barycenter is located within the Earth. The reason is exactly the same – the Earth doesn't ROTATE around the barycenter (the Earth rotates only around its own axis of rotation), but instead the Earth moves through space (around the barycenter) as one solid object. This object (the solid rock plus the mass of water) is held together by the Earth's gravity. The gravity of the Moon is very weak when compared to the gravity of the Earth, so the gravity of the Moon can only slightly deform the gravity of the Earth. Obviously this effect is strongest when the Earth, the Moon and the ocean are in the same line, so in the parts of the Earth that are farther away from the Earth-Moon line the effect is weaker. It slightly deforms the Earth in the Earth-Moon line (mostly the mass of water on the surface of the solid rock). It can be compared to a cherry (with the stone still inside) that you squeeze with your fingers. The cherry can be slightly squeezed, but it doesn't break just because you squeeze it AND you can't squeeze the stone inside.
I found a great visualization of the centrifugal force when the Earth is orbiting the Earth-Moon barycenter on this site:
https://beltoforion.de/article.php?a=tides_explained&p=orbital_motion
Here's a screenshot from that site:
We know that the Earth is orbiting the Earth-Moon barycenter, so in the middle of the Earth the centrifugal force is equal to the Moon's force of gravity. Let's see how it looks at the oceans:
Here's a biger picture (click to enlarge):
The point is that the force of gravity is stronger when the object is closer to the mass. The “right” ocean is closer to the Moon and the “left” ocean is farther away from the Moon. Because the centrifugal force is the same for all parts of the Earth, there are small differences (red arrows) at the opposite sides of the Earth, pointing in different directions. These are the forces that stretch the Earth (mostly the mass of water on the surface of the solid rock). As I said earlier – everything is held together by the gravity of the Earth, only slightly deformed by the gravity of the Moon.
4. Spacetime.
To understand why the force of gravity itself can be seen as a fictitious/pseudo force we have to understand the concept of spacetime – the three dimensions of space combined with the one dimension of time. Without any mass the spacetime can be imagined as a flat surface. Any non-zero mass curves spacetime and the force of gravity is just a result of the curved spacetime:
Please, notice that both the Earth and the Moon curve the spacetime (it reflects the fact that there are two forces of gravity – two accelerations).
The concept of curved spacetime came with the general theory of relativity (published by Albert Einstein in 1915) that had some spectacular predictions. One of them was the prediction that light itself should be “deflected”. A 1919 expedition led by Eddington confirmed general relativity's prediction for the “deflection” of starlight by the Sun during the total solar eclipse of May 29, 1919, making Einstein instantly famous. It can bee imagined like this:
The yellow line is the real path of the light and the red dashed line is the apparent position of the star. The apparent position is known to be wrong because it doesn't match the position of the star when looking from the Earth without the sun being in the way.
Please, notice that light doesn't actually bend – it is the spacetime that is bent. Light always travels in a straight line. Below there is another picture with an additional yellow line that is also STRAIGHT (in the curved spacetime):
Somebody could ask: “If the yellow lines are straight (in spacetime) then any space object (for example a comet) should go the same paths, right?” Wrong. Light is massless, so it doesn't bend the spacetime on its own, but any object with non-zero mass curves the spacetime IN ADDITION to the curvature caused by the main mass – the straight line for the non-zero mass object passing close to a star would be different (more “bent”):
Please, notice that the beginning of the green path (of the non-zero mass object) was the same as the beginning of the yellow path (of light) – in the “flat” spacetime the straight line is the same for any object.
The line around the more massive object is also a straight line for the less massive object (when both masses curve the same part of the spacetime at the same time):
If an object's mass was big enough it would be a black hole – the spacetime around it would be so bent that the straight line for the massless light would actually “circle” the object:
Here's a great video showing why the gravity and the curved spacetime are the same:
What makes the concept of spacetime much more difficult to grasp is the fact that according to the general theory of relativity objects within an accelerating enclosure behave similarly to objects in a gravitational field. For example, an observer will see a ball fall the same way in a rocket as it does on the Earth, provided that the acceleration of the rocket is equal to the acceleration due to the gravity at the surface of the Earth:
In fact an observer would have no way of deciding if he is on the Earth or in a rocket, if he were placed in a closed room. OR an observer in a rocket would have no way of deciding if the rocket is accelerating in space or just standing on the Earth:
The opposite is also true – a person who were in an elevator cabin falling down the elevator shaft would feel weightless, similar to a person in space who is not accelerating:
Well, this is a kind of simplification because this “rule” is true only for a small elevator cabin. However, in a HUGE elevator cabin you could actually tell that you are not in space because you could you see that the falling objects are getting closer to each other (farther away from the walls):
I tried to find an example of how acceleration bends the spacetime, but I couldn't find even a SINGLE one! There are many examples of how mass bends the spacetime, but NO examples how acceleration bends spacetime. I imagine this process to be similar to a car accelerating on a muddy road. To make my example even more interesting I added a ball lying some distance behind the car. Here's the state before acceleration (the spacetime is “flat”):
When the car starts accelerating its wheels dig into the ground and move the ground behind the car. The car moves in one direction, but the ground piles up behind the car, so the red ball finds itself on a slope, which makes it roll downhill in the opposite direction than the car:
I have no idea if my example is correct, but it definitely makes some sense. The antigravity effects (the slopes ABOVE the “flat” spacetime) might explain the fact that the universe is expanding.
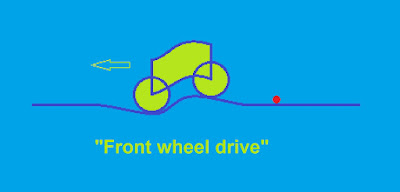
What kept bothering me, however, was the fact that a car accelerating on a muddy road would behave differently with different wheel drives (rear wheel drive, front wheel drive and 4x4 wheel drive). I wonder if this could be important in space when the acceleration would be big enough and the spaceship would be long enough. If that's the case then the spacetime together with the spaceship would bend differently with a “front wheel drive”:
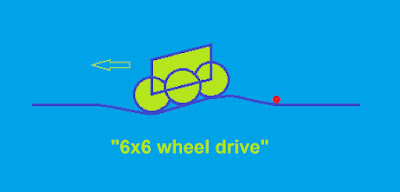
The rear wheels would be rolling “uphill”, which would consume energy. So the most efficient way of designing a spaceship would be to add another pair of “wheels” and make it “6x6 wheel drive”:
AGAIN: these examples are only how I myself imagine the way acceleration bends the spacetime. I have no idea if this analogy is actually correct. But this theory of mine is kind of fascinating.
5. Time.
Even more surprising aspect of the general theory of relativity is the fact that time “slows down” near massive objects. It was actually verified experimentally. The effect is significant enough that the Global Positioning System's artificial satellites need to have their clocks corrected. But how it can be imagined? This is actually much more easy than I thought, but I had to make my own examples again – the examples on the Internet usually have “too flat a bottom”. The point of my examples is to show you that the spacetime is bent (or “stretched”) the most in the point closest to the mass.
The yellow dots may be seen (or heard) as ticks of a clock. In the “flat” spacetime the ticks are regular, but near the massive objects the pauses between the ticks are longer and longer. This is connected with the crucial assumption (both in the general theory of relativity, as well as in the special theory of relativity) that any observer (on any path) should measure the same speed of light.
If mass/acceleration would be big enough and the spaceship would be long enough the clocks inside the same spaceship would run differently. In the example with big rockets (one accelerating in space and one standing on the Earth) you can see two clocks (A and B) showing different times (in both rockets).
My thought experiment with the antigravity twist made me wonder if time would slow down in such places (“above the flat spacetime”) too. Logic says it would:
Subscribe to:
Post Comments (Atom)




































No comments:
Post a Comment